SQL Server Bergabung dengan Estimasi menggunakan Histogram Coarse Alignment

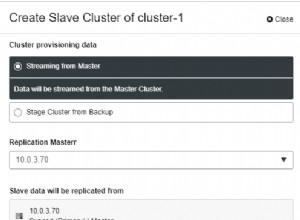
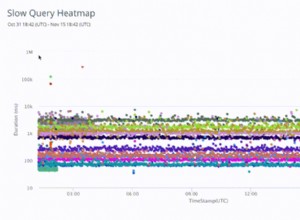
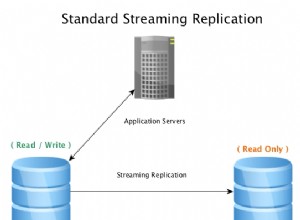
Perubahan utama yang dibuat pada Estimasi Kardinalitas yang dimulai dengan rilis SQL Server 2014 dijelaskan dalam Buku Putih Microsoft Mengoptimalkan Rencana Kueri Anda dengan Penaksir Kardinalitas SQL Server 2014 oleh Joe Sack, Yi Fang, dan Vassilis Papadimos.

Salah satu perubahan tersebut menyangkut estimasi gabungan sederhana dengan predikat persamaan atau ketidaksamaan tunggal menggunakan histogram statistik. Pada bagian berjudul "Join Estimate Algorithm Changes", makalah ini memperkenalkan konsep "coarse alignment" menggunakan batas histogram minimum dan maksimum:

Meskipun berpotensi kurang konsisten, CE warisan dapat menghasilkan perkiraan kondisi gabungan sederhana yang sedikit lebih baik karena penyelarasan histogram langkah demi langkah. CE baru menggunakan perataan kasar. Namun, perbedaan perkiraan mungkin cukup kecil sehingga kecil kemungkinannya menyebabkan masalah kualitas rencana.

Sebagai salah satu peninjau teknis makalah ini, saya merasa bahwa sedikit lebih banyak detail seputar perubahan ini akan berguna, tetapi itu tidak membuatnya menjadi versi final. Artikel ini menambahkan beberapa detail itu.

Contoh Perataan Histogram Kasar

Perataan kasar contoh di White Paper menggunakan versi Data Warehouse dari database sampel AdventureWorks. Terlepas dari namanya, databasenya agak kecil; cadangan hanya 22,3MB dan berkembang menjadi sekitar 200MB. Itu dapat diunduh melalui tautan di halaman dokumentasi Instalasi dan Konfigurasi AdventureWorks.

Kueri yang kami minati bergabung dengan FactResellerSales dan FactCurrencyRate tabel.

SELECT
    FRS.ProductKey,
    FRS.OrderDateKey,
    FRS.DueDateKey,
    FRS.ShipDateKey,
    FCR.DateKey,
    FCR.AverageRate,
    FCR.EndOfDayRate,
    FCR.[Date]
FROM dbo.FactResellerSales AS FRS
JOIN dbo.FactCurrencyRate AS FCR
    ON FCR.CurrencyKey = FRS.CurrencyKey;

Ini adalah penggabungan sederhana pada satu kolom sehingga memenuhi syarat untuk estimasi gabungan kardinalitas dan selektivitas menggunakan keselarasan kasar histogram.

Histogram

Histogram yang kita butuhkan terkait dengan CurrencyKey kolom pada setiap tabel yang digabungkan. Pada salinan baru database AdventureWorksDW, statistik yang sudah ada sebelumnya untuk FactResellerSales yang lebih besar tabel didasarkan pada sampel. Untuk memaksimalkan reproduktifitas dan membuat perhitungan terperinci sesederhana mungkin untuk diikuti (menghindari penskalaan), hal pertama yang akan kita lakukan adalah menyegarkan statistik menggunakan pemindaian penuh:

UPDATE STATISTICS dbo.FactCurrencyRate WITH FULLSCAN;
UPDATE STATISTICS dbo.FactResellerSales WITH FULLSCAN;

Tabel ini memiliki manfaat ramah-demo untuk membuat maxdiff yang kecil dan sederhana histogram:

DBCC SHOW_STATISTICS
    (FactResellerSales, CurrencyKey)
WITH HISTOGRAM;
 
DBCC SHOW_STATISTICS
    (FactCurrencyRate, [PK_FactCurrencyRate_CurrencyKey_DateKey])
WITH HISTOGRAM;

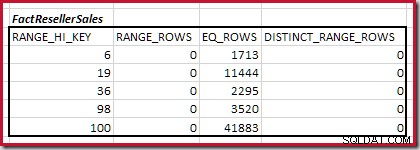
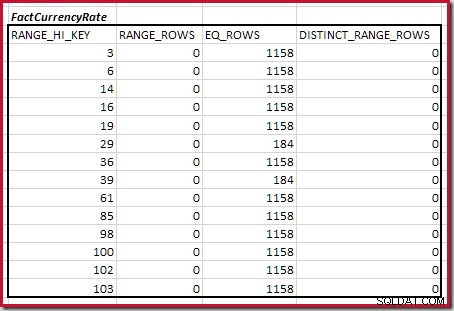
Menggabungkan Langkah Histogram Pencocokan Minimum

Langkah pertama dalam perataan kasar perhitungannya adalah untuk mencari kontribusi terhadap kardinalitas gabungan yang diberikan oleh langkah histogram pencocokan terendah. Untuk contoh histogram kami, nilai langkah pencocokan minimum ada di RANGE_HI_KEY = 6 :

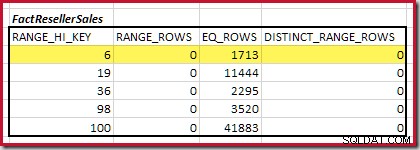
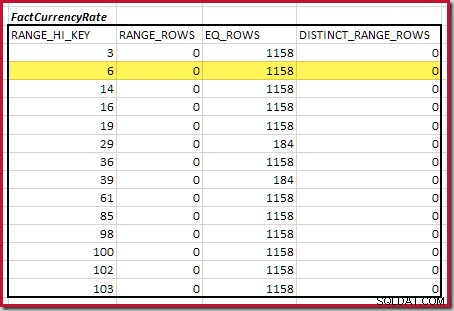
Perkiraan kardinalitas equijoin hanya untuk langkah yang disorot ini adalah 1.713 * 1.158 =1.983.654 baris .

Sisa Langkah yang Sesuai

Selanjutnya, kita perlu mengidentifikasi rentang histogram RANGE_HI_KEY melangkah ke maksimum untuk kemungkinan pertandingan equijoin. Ini melibatkan bergerak maju dari minimum yang ditemukan sebelumnya sampai salah satu input histogram kehabisan baris. Rentang equijoin yang cocok untuk contoh saat ini disorot di bawah ini:

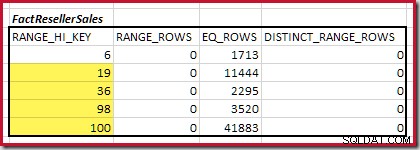
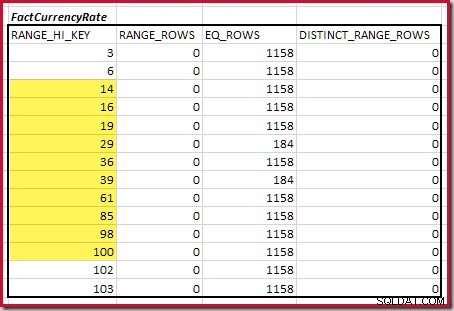
Kedua rentang ini mewakili baris yang tersisa yang mungkin diharapkan berkontribusi pada kardinalitas equijoin.

Estimasi Berbasis Frekuensi Kasar

Pertanyaannya sekarang adalah bagaimana melakukan kasar estimasi kardinalitas equijoin dari langkah-langkah yang disorot, menggunakan informasi yang tersedia.

Penaksir kardinalitas asli akan melakukan penyelarasan histogram langkah demi langkah yang halus menggunakan interpolasi linier, menilai kontribusi gabungan dari setiap langkah (seperti yang kami lakukan untuk nilai langkah minimum sebelumnya), dan menjumlahkan setiap kontribusi langkah untuk memperoleh perkiraan bergabung penuh. Meskipun prosedur ini sangat masuk akal secara intuitif, pengalaman praktisnya adalah bahwa pendekatan berbutir halus ini menambahkan overhead komputasi dan dapat menghasilkan hasil dengan kualitas yang bervariasi.

Penaksir asli memiliki cara lain untuk memperkirakan kardinalitas gabungan ketika informasi histogram tidak tersedia, atau dinilai secara heuristik lebih rendah. Ini dikenal sebagai estimasi berbasis frekuensi, dan menggunakan definisi berikut:

• C – kardinalitas (jumlah baris)
• D – jumlah nilai yang berbeda
• F – frekuensi (jumlah baris) untuk setiap nilai yang berbeda
• Catatan C =D * F menurut definisi

Pengaruh equijoin dari relasi R1 dan R2 pada masing-masing properti ini adalah seperti yang ditunjukkan di bawah ini:

• F' =F1 * F2
• D' =MIN(D1; D2) – dengan asumsi penahanan
• C' =D' * F' (sekali lagi, menurut definisi)

Kami mengejar C', kardinalitas equijoin. Mengganti D' dan F' dalam rumus, dan memperluas:

• C' =D' * F'
• C' =MIN(D1; D2) * F1 * F2
• C' =MIN(D1 * F1 * F2; D2 * F1 * F2)
• sekarang, karena C1 =D1 * F1, dan C2 =D2 * F2:
• C' =MIN(C1 * F2, C2 * F1)
• akhirnya, karena F =C/D (juga menurut definisi):
• C' =MIN(C1 * C2 / D2; C2 * C1 / D1)

Perhatikan bahwa C1 * C2 adalah produk dari dua kardinalitas input (Cartesian join), jelas bahwa minimum dari ekspresi tersebut akan menjadi satu dengan jumlah nilai yang berbeda yang lebih tinggi:

• C' =(C1 * C2) / MAX(D1; D2)

Dalam hal ini semua tampak sedikit abstrak, cara intuitif untuk berpikir tentang estimasi equijoin berbasis frekuensi adalah dengan mempertimbangkan bahwa setiap nilai yang berbeda dari satu relasi akan bergabung dengan sejumlah baris (frekuensi rata-rata) dalam relasi lainnya. Jika kita memiliki 5 nilai berbeda di satu sisi, dan setiap nilai berbeda di sisi lain muncul rata-rata 3 kali, perkiraan equijoin yang masuk akal (tetapi kasar) adalah 5 * 3 =15.

Ini bukan kuas yang begitu luas seperti yang terlihat. Ingat kardinalitas dan nilai-nilai yang berbeda angka di atas tidak berasal dari seluruh relasi, tetapi hanya dari langkah pencocokan di atas minimum. Oleh karena itu estimasi kasar antara nilai minimum dan maksimum.

Perhitungan Frekuensi

Kita bisa mendapatkan masing-masing parameter ini dari langkah-langkah histogram yang disorot.

• Kardinalitas C adalah jumlah dari EQ_ROWS dan RANGE_ROWS .
• Jumlah nilai yang berbeda D adalah jumlah dari DISTINCT_RANGE_ROWS ditambah satu untuk setiap langkah.

Kardinalitas C1 dari pencocokan FactResellerSales langkah adalah jumlah sel yang disorot:

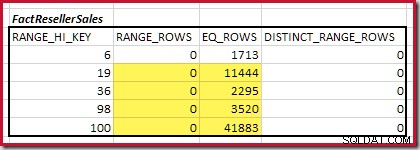
Ini memberikan C1 =59.142 baris.

Tidak ada baris rentang yang berbeda, jadi satu-satunya nilai yang berbeda berasal dari empat batas langkah itu sendiri, memberikan D1 =4 .

Untuk tabel kedua:

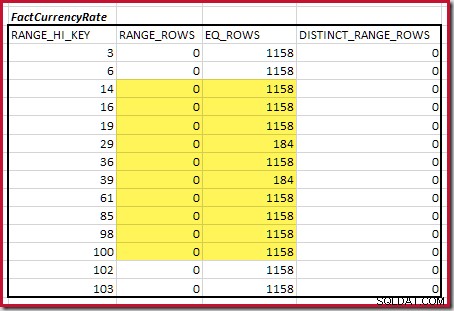
Ini memberikan C2 =9.632 . Sekali lagi tidak ada baris rentang yang berbeda, sehingga nilai yang berbeda berasal dari batas sepuluh langkah, D2 =10.

Melengkapi Estimasi Equijoin

Kami sekarang memiliki semua angka yang kami butuhkan untuk rumus equijoin:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(59142 * 9632) / MAX(4; 10)
• C' =569655744 / 10
• C' =56.965.574.4

Ingat, ini adalah kontribusi langkah-langkah histogram di atas batas kecocokan minimum. Untuk melengkapi estimasi kardinalitas gabungan, kita perlu menambahkan kontribusi dari nilai langkah pencocokan minimum, yaitu 1.713 * 1.158 =1.983.654 baris.

Oleh karena itu, perkiraan equijoin akhir adalah 56.965.574.4 + 1.983.654 =58.949.228,4 baris atau 58.949.200 sampai enam angka penting.

Hasil ini dikonfirmasi dalam perkiraan rencana eksekusi untuk kueri sumber:

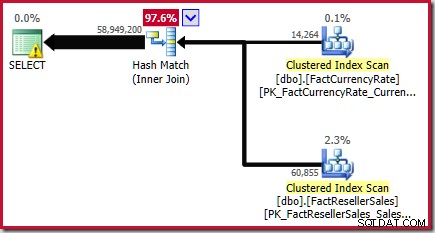
Sebagaimana dicatat dalam Buku Putih, ini bukan perkiraan yang bagus. Jumlah sebenarnya dari baris yang dikembalikan oleh kueri ini adalah 70.470.090 . Estimasi yang dihasilkan oleh penaksir kardinalitas asli ("warisan") – menggunakan penyelarasan histogram langkah demi langkah – adalah 70.470.100 baris.

Hasil yang lebih baik seringkali dimungkinkan dengan metode yang lebih baik, tetapi hanya jika statistik merupakan representasi yang sangat baik dari distribusi data yang mendasarinya. Ini bukan hanya soal menjaga agar statistik tetap mutakhir, atau menggunakan populasi pemindaian penuh. Algoritme yang digunakan untuk mengemas informasi ke dalam maksimum 201 langkah histogram tidaklah sempurna, dan dalam banyak kasus, banyak distribusi data dunia nyata tidak mampu melakukan fidelitas histogram seperti itu. Rata-rata, orang harus menemukan bahwa metode yang lebih kasar memberikan estimasi yang sangat memadai dan stabilitas yang lebih besar dengan CE baru.

Contoh Kedua

Ini sedikit dibangun di atas contoh sebelumnya, dan tidak memerlukan unduhan database sampel.

DROP TABLE IF EXISTS
    dbo.R1,
    dbo.R2;
 
CREATE TABLE dbo.R1 (n integer NOT NULL);
CREATE TABLE dbo.R2 (n integer NOT NULL);
 
INSERT dbo.R1
    (n)
VALUES
    (1), (2), (3), (4), (5), (6), (7), (8), (9), (10),
    (6), (6), (6), (6), (6), (6), (6), (6), (6), (6), 
    (6), (6), (6), (6), (6), (6), (6), (6), (6);
 
INSERT dbo.R2
    (n)
VALUES
    (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15),
    (10), (10);
 
CREATE STATISTICS stats_n ON dbo.R1 (n) WITH FULLSCAN;
CREATE STATISTICS stats_n ON dbo.R2 (n) WITH FULLSCAN;

Histogram yang menunjukkan langkah-langkah minimum yang cocok adalah:

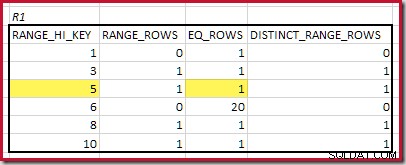
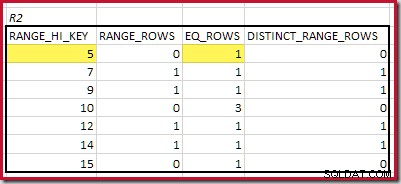
RANGE_HI_KEY terendah yang cocok adalah 5. Nilai EQ_ROWS keduanya adalah 1, jadi perkiraan kardinalitas equijoin adalah 1 * 1 =1 baris .

RANGE_HI_KEY yang paling cocok adalah 10. Menyoroti baris histogram R1 untuk estimasi berbasis frekuensi kasar:

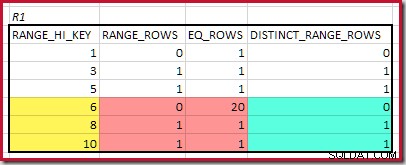
Menjumlahkan EQ_ROWS dan RANGE_ROWS memberikan C1 =24 . Jumlah baris yang berbeda adalah 2 DISTINCT_RANGE_ROWS (nilai berbeda di antara langkah) ditambah 3 untuk nilai berbeda yang terkait dengan setiap batas langkah, menghasilkan D1 =5 .

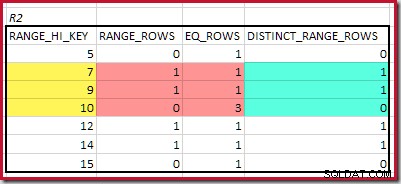
Untuk R2, menjumlahkan EQ_ROWS dan RANGE_ROWS memberikan C2 =7 . Jumlah baris yang berbeda adalah 2 DISTINCT_RANGE_ROWS (nilai berbeda antara langkah) ditambah 3 untuk nilai berbeda yang terkait dengan setiap batas langkah, menghasilkan D2 =5 .

Estimasi equijoin C' adalah:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(24 * 7) / 5
• C' =33.6

Menambahkan di 1 baris dari kecocokan langkah minimum memberikan perkiraan total 34,6 baris untuk equijoin:

SELECT
    R1.n,
    R2.n
FROM dbo.R1 AS R1
JOIN dbo.R2 AS R2
    ON R2.n = R1.n;

Perkiraan rencana eksekusi menunjukkan perkiraan yang cocok dengan perhitungan kami:

Ini tidak sepenuhnya benar, tetapi penaksir kardinalitas "warisan" tidak lebih baik, memperkirakan 15,25 baris versus 27 aktual:

Untuk perawatan yang lengkap, kami juga harus menambahkan kontribusi akhir dari pencocokan langkah-langkah null histogram, tetapi ini tidak umum untuk equijoin (yang biasanya ditulis untuk menolak nol) dan ekstensi yang relatif mudah bagi pembaca yang tertarik.

Pemikiran Terakhir

Semoga rincian dalam artikel ini akan mengisi beberapa celah bagi siapa saja yang pernah bertanya-tanya tentang "kesejajaran kasar". Perhatikan bahwa ini hanyalah salah satu komponen kecil dalam penduga kardinalitas. Ada beberapa konsep dan algoritme penting lainnya yang digunakan untuk estimasi gabungan, terutama cara penilaian predikat non-gabungan, dan bagaimana gabungan yang lebih kompleks ditangani. Banyak bagian yang sangat penting tercakup dengan cukup baik dalam Buku Putih.