Mengembalikan Kombinasi
Menggunakan tabel angka atau CTE penghasil angka, pilih 0 hingga 2^n - 1. Menggunakan posisi bit yang mengandung 1 dalam angka-angka ini untuk menunjukkan ada atau tidak adanya anggota relatif dalam kombinasi, dan menghilangkan yang tidak memiliki jumlah nilai yang benar, Anda harus dapat mengembalikan set hasil dengan semua kombinasi yang Anda inginkan.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Kueri ini berkinerja cukup baik, tetapi saya memikirkan cara untuk mengoptimalkannya, menyalin dari Jumlah Bit Paralel yang Bagus untuk terlebih dahulu mendapatkan jumlah item yang tepat diambil pada suatu waktu. Ini bekerja 3 hingga 3,5 kali lebih cepat (baik CPU maupun waktu):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Saya pergi dan membaca halaman penghitungan bit dan berpikir bahwa ini dapat bekerja lebih baik jika saya tidak melakukan % 255 tetapi melanjutkan dengan aritmatika bit. Ketika saya mendapat kesempatan, saya akan mencobanya dan melihat bagaimana hasilnya.
Klaim kinerja saya didasarkan pada kueri yang dijalankan tanpa klausa ORDER BY. Untuk kejelasan, apa yang dilakukan kode ini adalah menghitung jumlah set 1-bit dalam Num dari Numbers meja. Itu karena angka digunakan sebagai semacam pengindeks untuk memilih elemen himpunan mana yang ada dalam kombinasi saat ini, sehingga jumlah 1-bit akan sama.
Saya harap Anda menyukainya!
Sebagai catatan, teknik menggunakan pola bit bilangan bulat untuk memilih anggota himpunan adalah apa yang saya ciptakan sebagai "Gabungan Silang Vertikal". Ini secara efektif menghasilkan gabungan silang dari beberapa set data, di mana jumlah set &gabungan silang adalah sewenang-wenang. Di sini, jumlah set adalah jumlah item yang diambil dalam satu waktu.
Sebenarnya penggabungan silang dalam pengertian horizontal biasa (menambahkan lebih banyak kolom ke daftar kolom yang ada dengan setiap gabungan) akan terlihat seperti ini:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Pertanyaan saya di atas secara efektif "gabung silang" sebanyak yang diperlukan dengan hanya satu gabung. Hasilnya tidak dipivot dibandingkan dengan gabungan silang yang sebenarnya, tentu saja, tapi itu masalah kecil.
Kritik terhadap Kode Anda
Pertama, bolehkah saya menyarankan perubahan ini pada UDF Faktorial Anda:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Sekarang Anda dapat menghitung kumpulan kombinasi yang jauh lebih besar, ditambah lagi lebih efisien. Anda bahkan mungkin mempertimbangkan untuk menggunakan decimal(38, 0) untuk memungkinkan penghitungan perantara yang lebih besar dalam penghitungan kombinasi Anda.
Kedua, kueri yang Anda berikan tidak mengembalikan hasil yang benar. Misalnya, menggunakan data pengujian saya dari pengujian kinerja di bawah, set 1 sama dengan set 18. Sepertinya kueri Anda mengambil garis geser yang membungkus:setiap set selalu 5 anggota yang berdekatan, terlihat seperti ini (saya memutar agar lebih mudah dilihat):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Bandingkan pola dari kueri saya:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Hanya untuk mengarahkan bit-pattern -> indeks kombinasi hal rumah bagi siapa saja yang tertarik, perhatikan bahwa 31 dalam biner =11111 dan polanya adalah ABCDE. 121 dalam biner adalah 1111001 dan polanya adalah A__DEFG (dipetakan ke belakang).
Hasil Performa Dengan Tabel Bilangan Riil
Saya menjalankan beberapa pengujian kinerja dengan set besar pada kueri kedua saya di atas. Saya tidak memiliki catatan saat ini tentang versi server yang digunakan. Ini data pengujian saya:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter menunjukkan bahwa "penggabungan silang vertikal" ini tidak berfungsi sebaik hanya menulis SQL dinamis untuk benar-benar melakukan CROSS JOIN yang dihindarinya. Dengan biaya sepele dari beberapa bacaan lagi, solusinya memiliki metrik antara 10 dan 17 kali lebih baik. Performa kuerinya menurun lebih cepat daripada kueri saya seiring bertambahnya jumlah pekerjaan, tetapi tidak cukup cepat untuk menghentikan siapa pun menggunakannya.
Kumpulan angka kedua di bawah ini adalah faktor yang dibagi dengan baris pertama dalam tabel, hanya untuk menunjukkan bagaimana skalanya.
Erik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Petrus
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Ekstrapolasi, akhirnya permintaan saya akan lebih murah (meskipun dari awal dibaca), tetapi tidak untuk waktu yang lama. Untuk menggunakan 21 item dalam set sudah membutuhkan tabel angka hingga 2097152...
Berikut adalah komentar yang awalnya saya buat sebelum menyadari bahwa solusi saya akan bekerja secara drastis lebih baik dengan tabel angka yang aktif:
Hasil Performa dengan Tabel Angka Saat Ini
Ketika saya awalnya menulis jawaban ini, saya berkata:
Yah, saya mencobanya, dan hasilnya kinerjanya jauh lebih baik! Berikut adalah kueri yang saya gunakan:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Perhatikan bahwa saya memilih nilai ke dalam variabel untuk mengurangi waktu dan memori yang diperlukan untuk menguji semuanya. Server masih melakukan semua pekerjaan yang sama. Saya memodifikasi versi Peter agar serupa, dan menghapus tambahan yang tidak perlu sehingga keduanya se-ramping mungkin. Versi server yang digunakan untuk pengujian ini adalah Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) berjalan di VM.
Di bawah ini adalah bagan yang menunjukkan kurva kinerja untuk nilai N dan K hingga 21. Data dasarnya ada di jawaban lain di halaman ini . Nilai tersebut merupakan hasil dari 5 run dari setiap kueri pada setiap nilai K dan N, diikuti dengan membuang nilai terbaik dan terburuk untuk setiap metrik dan rata-rata 3 sisanya.
Pada dasarnya, versi saya memiliki "bahu" (di sudut paling kiri grafik) pada nilai N tinggi dan nilai K rendah yang membuatnya berkinerja lebih buruk daripada versi SQL dinamis. Namun, ini tetap cukup rendah dan konstan, dan puncak pusat di sekitar N =21 dan K =11 jauh lebih rendah untuk Durasi, CPU, dan Bacaan daripada versi SQL dinamis.
Saya menyertakan bagan jumlah baris yang diharapkan untuk dikembalikan setiap item sehingga Anda dapat melihat bagaimana kinerja kueri ditumpuk dengan seberapa besar tugas yang harus dilakukan.
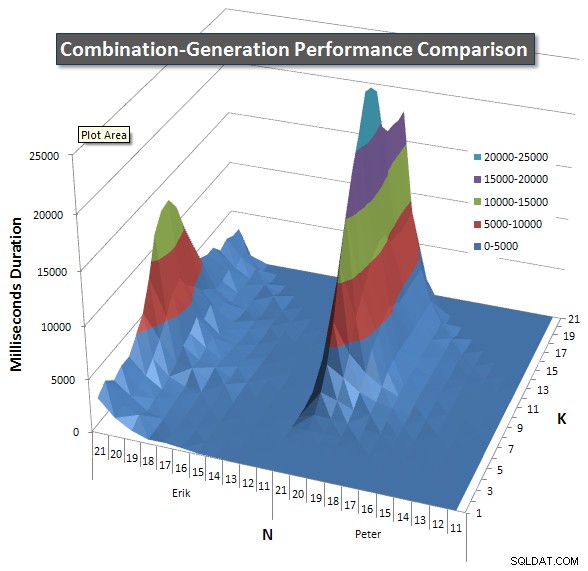
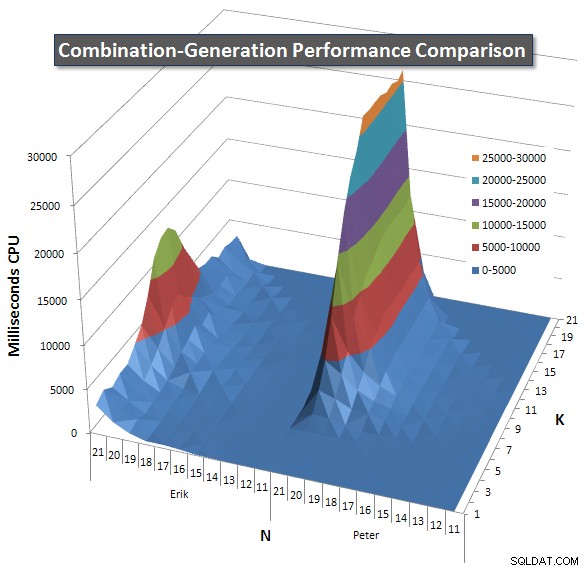
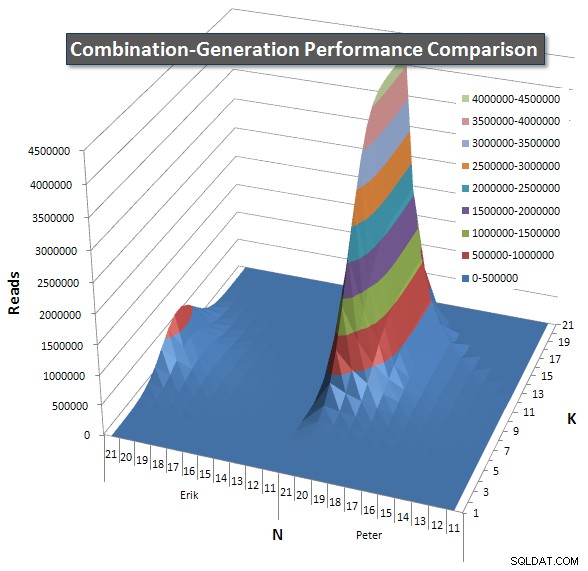
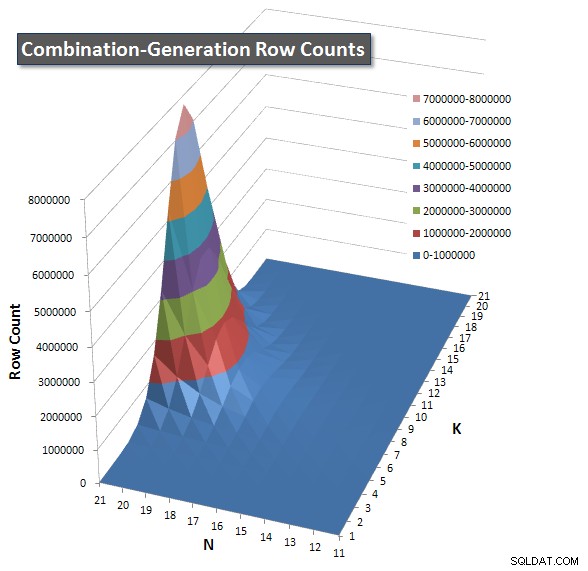
Silakan lihat jawaban tambahan saya di halaman ini untuk hasil kinerja yang lengkap. Saya mencapai batas karakter posting dan tidak dapat memasukkannya di sini. (Ada ide di mana lagi untuk meletakkannya?) Untuk menempatkan hal-hal dalam perspektif terhadap hasil kinerja versi pertama saya, berikut format yang sama seperti sebelumnya:
Erik
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Petrus
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Kesimpulan
- Tabel angka langsung lebih baik daripada tabel nyata yang berisi baris, karena membaca satu pada jumlah baris yang besar membutuhkan banyak I/O. Lebih baik menggunakan sedikit CPU.
- Pengujian awal saya tidak cukup luas untuk benar-benar menunjukkan karakteristik kinerja kedua versi.
- Versi Peter dapat ditingkatkan dengan membuat setiap JOIN tidak hanya lebih besar dari item sebelumnya, tetapi juga membatasi nilai maksimum berdasarkan berapa banyak item yang harus masuk ke dalam set. Misalnya, pada 21 item yang diambil 21 sekaligus, hanya ada satu jawaban dari 21 baris (semua 21 item, satu kali), tetapi rowset perantara dalam versi SQL dinamis, di awal rencana eksekusi, berisi kombinasi seperti " AU" pada langkah 2 meskipun ini akan dibuang pada penggabungan berikutnya karena tidak ada nilai yang lebih tinggi dari "U" yang tersedia. Demikian pula, rowset perantara pada langkah 5 akan berisi "ARSTU" tetapi satu-satunya kombo yang valid pada saat ini adalah "ABCDE". Versi yang ditingkatkan ini tidak akan memiliki puncak yang lebih rendah di tengah, jadi mungkin tidak cukup meningkatkannya untuk menjadi pemenang yang jelas, tetapi setidaknya akan menjadi simetris sehingga grafik tidak akan tetap maksimal melewati bagian tengah wilayah tetapi akan jatuh kembali mendekati 0 seperti yang dilakukan versi saya (lihat sudut atas puncak untuk setiap kueri).
Analisis Durasi
- Tidak ada perbedaan yang sangat signifikan antara versi dalam durasi (>100ms) hingga 14 item diambil 12 sekaligus. Sampai saat ini, versi saya menang 30 kali dan versi SQL dinamis menang 43 kali.
- Mulai 14•12, versi saya lebih cepat 65 kali (59>100 md), versi SQL dinamis 64 kali (60>100 md). Namun, setiap kali versi saya lebih cepat, itu menghemat total durasi rata-rata 256,5 detik, dan ketika versi SQL dinamis lebih cepat, itu menghemat 80,2 detik.
- Total durasi rata-rata untuk semua percobaan adalah Erik 270,3 detik, Peter 446,2 detik.
- Jika tabel pencarian dibuat untuk menentukan versi mana yang akan digunakan (memilih yang lebih cepat untuk input), semua hasil dapat dilakukan dalam 188,7 detik. Menggunakan yang paling lambat setiap kali akan memakan waktu 527,7 detik.
Membaca Analisis
Analisis durasi menunjukkan kueri saya menang dengan jumlah yang signifikan tetapi tidak terlalu besar. Saat metrik dialihkan ke pembacaan, gambaran yang sangat berbeda muncul--kueri saya menggunakan rata-rata 1/10 pembacaan.
- Tidak ada perbedaan yang sangat signifikan antara versi dalam pembacaan (>1000) hingga 9 item diambil 9 sekaligus. Sampai saat ini, versi saya menang 30 kali dan versi SQL dinamis menang 17 kali.
- Mulai 9•9, versi saya menggunakan lebih sedikit pembacaan 118 kali (113>1000), versi SQL dinamis 69 kali (31>1000). Namun, setiap kali versi saya menggunakan lebih sedikit pembacaan, ini menghemat total rata-rata 75,9 juta pembacaan, dan ketika versi SQL dinamis lebih cepat, menghemat 380 ribu pembacaan.
- Total rata-rata pembacaan untuk semua uji coba adalah Erik 8.4M, Peter 84M.
- Jika tabel pencarian dibuat untuk menentukan versi mana yang akan digunakan (memilih yang terbaik untuk input), semua hasil dapat dilakukan dalam 8 juta pembacaan. Menggunakan yang terburuk setiap kali akan membutuhkan 84,3 juta pembacaan.
Saya akan sangat tertarik untuk melihat hasil versi SQL dinamis yang diperbarui yang menempatkan batas atas ekstra pada item yang dipilih pada setiap langkah seperti yang saya jelaskan di atas.
Tambahan
Versi kueri saya berikut mencapai peningkatan sekitar 2,25% dari hasil kinerja yang tercantum di atas. Saya menggunakan metode penghitungan bit HAKMEM MIT, dan menambahkan Convert(int) pada hasil row_number() karena mengembalikan bigint. Tentu saja saya berharap ini adalah versi yang saya gunakan untuk semua pengujian kinerja dan bagan serta data di atas, tetapi sepertinya saya tidak akan pernah mengulanginya karena padat karya.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
Dan saya tidak dapat menahan diri untuk tidak menampilkan satu versi lagi yang melakukan pencarian untuk mendapatkan jumlah bit. Bahkan mungkin lebih cepat daripada versi lain:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))