Jika Anda mencari algoritma aproksimasi, saya sarankan untuk mencari algoritma k-means atau cluster hierarkis, terutama kurva monster atau kurva pengisian ruang. Pertama Anda dapat menghitung pohon merentang minimal dari grafik dan kemudian menghapus tepi terpanjang dan termahal. Kemudian pohon tersebut membuat banyak pohon kecil dan Anda dapat menggunakan k-means untuk menghitung kelompok titik yaitu cluster.
"Algoritme k-clustering tautan tunggal ... persisnya adalah algoritme Kruskal ... setara dengan menemukan MST dan menghapus tepi paling mahal k-1." Lihat misalnya di sini:https://stats.stackexchange.com/ pertanyaan/1475/visualization-software-for-clustering .
Contoh yang baik untuk kurva monster adalah kurva hilbert. Bentuk dasar kurva ini adalah bentuk-U dan dengan menyalin banyak darinya bersama-sama dan memutarnya, kurva mengisi ruang euklidian. Anehnya kode abu-abu dapat membantu untuk mengetahui orientasi bentuk-U ini. Anda dapat mencari kurva hilbert quadtree indeks spasial Nick artikel blog tentang detail selengkapnya . Alih-alih menghitung indeks kurva, Anda dapat menyusun quadkey seperti di peta bing. Quadkey unik untuk setiap koordinat dan dapat digunakan dengan operasi string normal. Setiap posisi di kunci adalah bagian dari kurva berbentuk U dan dengan demikian Anda dapat memilih wilayah titik ini dari pilih sebagian dari kiri ke kanan dari quadkey.
Pada gambar ini Anda dapat melihat poligon hijau ditemukan menggunakan kurva hilbert:
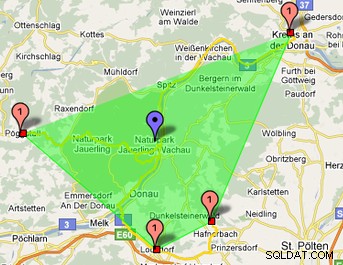
Anda dapat menemukan kelas php saya di sini:https://www.phpclasses.org/package/6202-PHP-Generate-points-of-an-Hilbert-curve.html